Batch 3 - Class 214 - Dr Square, Digital Roots
HTML Content
Pre-Class Exercise
- (Geoffrey - 143) Three dutchmen and their wives go shopping hogs, and each buys as many hogs as he or she pays for each hog. Each husband spends Rs 63 more than respective wife. Husbands are Hendrick, Elas and Cornelius. Wives are Gurtrun, Katrun and Anna. Hendrick buys 23 more hogs than Katrun, while Elas buys 11 more than Gurtrun. What are the names of each man's wife?
- Answer: Pairs are 32/31, 12/9, and 8/1 - we can now see integers that differ by 23 and 11. So its Hendrick-Anna, Elas-Katrun and Cornelius-Gurtrun
Attendance Rhea, Aashvi, Kabir, Angad, Rehaan, Kushagra
Class puzzles
Let’s take the number 26. Squaring it gives 676. The digital sum of 676 is 19. Squaring gives 361. Digital sum of 361 is 10. Squaring 10 gives 100. Digital sum of 100 is 1. Squaring gives 1. Digital sum gives 1. So we stay at 1 forever once we get there.
More briefly, we could write 26 –> 676 –> 19 –> 10 –> 100 –> 1 –> 1 –> 1 –> etc.
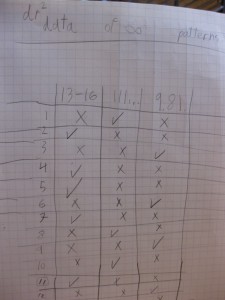
We called this the 1 loop. Do the same exercise for all numbers, and see what kind of loops do you discover. Do you see any patterns?
We discovered three loops so far, which we’ve called the 1 loop, the 13-16 loop (13–>169–>16–>256–>13), and the 9 loop (9–>81–>9). While we conjecture that these are the only three loops, we don’t have a proof yet.
- Are there just three loops? Or are there others that we haven’t discovered yet? How can you prove it?
- Is there a quick way to see which loop a number will end up in?
- Will every number end up in a loop? Is it possible that something else could happen?
Let kids work through it. Some of them may have hypotheses. Take a diversion towards Digital Roots. Check if they have heard of it before.
- "Digital root" of a number is the result you get if you add up its digits, and then add up the digits of that result, and so on, till you get to a single digit.
- Illustrate digital root of 44689 - Answer: 4
- Lets look at two numbers that add up to 44689 - such as 31847 and 12842 - what is the relationship between the digital roots of these numbers?
- What about two numbers that subtract to make 44689, like 83491 and 38802? Is there a relationship between their digital roots? What can you do with 100000 and 55311?
- What about two numbers that multiply to make 44689, like 67 and 667? or 23 and 1943?
- What happens to digital root if you multiple a number by 9?
- What happens to digital root if you add 9 to a number?
- The process of taking the digital roots is called "Casting out Nines" - why? Do we really cast away all nines?
Applying Digital Roots to check Arithmetic
- One use of casting is to check arithmetic quickly. If the digital root doesn't match up, then there was an arithmetic mistake. Check the following? Are the other ones actually correct?
- 1234+5678=6812
- 12345-9876=2469
- 10101-2468=7623
- 1234 * 5678 = 7006652
- 4321 * 8765 = 37783565
- 345 * 543 = 196335
- 2^17 = 130072 (How should we handle exponents?)
- Some kinds of mistakes will never be found by casting out nines. Give some examples
- Does this work for division? How can we rewrite division as multiplication and addition, so that we could check by casting out nines? For example: 23894 divided by 82 is 291 with a remainder of 32?
- What is the digital root of 3726125? Is 3726125 a perfect square?
- Lets do a calculator trick - lets pass around the calculator and every kid will press a random digit and multiply key. Once we have done that 25 times, there will be a number on the screen. Another kid will now eliminate one digit (not a 0), and yet another kid will jumble up the digits and write them. A mathematician can tell the missing digit. How?
- Answer: Mathematician assume the digital root of final number is 9, which will be the case if anyone had pressed a 9, or two people had pressed 3 or 6. This can go wrong in some cases though.
Now lets come back to the original problem.
What are some properties of Digital Roots with respect to this problem?
- Try to see a pattern on which cycle the number gets into with respect to its digital root.
- What is the relationship between digit sum mod 9, and the number itself? What if we square in mod 9?
- What happens to the digital root if you square the number? Which cycle is it likely to get into? Can you prove the cycle behavior on squaring the number?
- What happens to the digital root if you add the digits? Does it matter if you add it once or repetitively? Can you show that squaring a number or squaring its digital root gives the same resultant cycle? i.e square of (10a+b) has the same cycle as square of (a+b)?
Homework
Dr Square Plus 1
- Choose a starting number. Square the number and then add 1. Sum up the digits. Repeat the process till you figure out what is going on. Can you find all the loops? Can you predict which loop the number will land up in?
References:
Mathematical Puzzles, Geoffrey Mott-Smith